

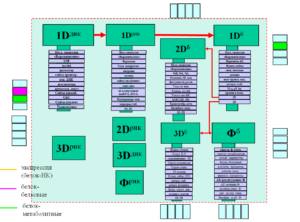
Определений термина “биоинформатика” очень много – от “менеджмента билогических данных” [1] до обработки всех данных на свете. Ядром биоинформатики является комплекс задач, лежащих в поле “центральной догмы” молекулярной биологии (см. Рис. вверху) и затрагивает вопросы взаимосвязи различных уровней описания (первичной, вторичной, третичной структур) биомакромолекул (ДНК, РНК, белок). Задачи биоинформатики состоят в нахождении наиболее эффективных способов перекодировки этих представлений: из первичной структуры получить вторичную, третичную и др.
За последние 40 лет в биоинформатике преобладают методы, основанные на анализе сходства молекул. Однако, международные конференции-соревнования по анализу данных о структурах белков показывают низкую эффективность алгоритмов, построенных с помощью методов анализа схожести.
Поэтому, в биоинформатике уже более 40 лет существует широкий класс не решённых задач, связанных с обработкой данных сотен тысяч пространственных структур белков, миллионов аминокислотных последовательностей, миллиардов нуклеотидных последовательностей. Известные в западной биоинформатике методы основаны на многочисленных “постулатах” (анализ “схожести” – только одно из направлений введения этих “постулатов”), подавляющее большинство из которых произвольны и не имеют четкого обоснования даже в самой проблемной области. В результате, повсеместно используемые в биоинформатике методы не обладают высокой специфичностью и селективностью распознавания и, с точки зрения практического биолога или врача, не представляют существенной практической ценности.
Например, те же повсеместно использующиеся методы установления функций генов и белков (т.н. «аннотация генома») основаны исключительно на анализе “схожести” нуклеотидных и аминокислотных последовательностей, причем используемые определения “схожести” основаны на произвольных предположениях вроде «общей подпоследовательности», произвольных отношениях эквивалентности символов алфавита (аминокислот), на пренебрежении контекстом символьных последовательностей и т. п. Как показал проведенный анализ литературы по данному вопросу, практическое применение сотен этих методов, например, к геному человека позволяет установить самую общую биологическую функцию не более, чем для 50% генов и белков: в настоящее время, аннотированно около 15,000 генов из 29,000.
Теория разрешимости позволяет взглянуть на проблему аннотации генома совершенно с иной точки зрения. В рамках математической методологии школы академика Ю.И.Журавлева (т.н. алгебраический подход к распознаванию) существует ряд задач, которые должны быть решены перед поиском “наилучшего” алгоритма (который, заметим, практически всегда проводится методом интуитивно-экспертного тыка). В частности, алгебраический подход подразумевает анализ условий существования любого алгоритма с учётом заданного способа признакового описания биомакромолекул. Для проведения этого анализа выводятся и тестируются теоремы существования, которые позволяют осуществлять эффективный поиск наиболее подходящих формальных постановок задач. Эффективность поиска существенно повышается при использовании методов топологического и метрического анализа данных.
Например, в случае задачи аннотации генома (которая, по сути, является задачей классификации символьных последовательностей) анализ теорем существования решений этой задачи позволяет получить целый диапазон трактабельных формальных постановок, к которым, затем, применяются алгоритмы алгебраического подхода. Решение этой задачи весьма актуально и востребовано – ведь число секвенированных геномов оценивается тысячами, а аннотировано (т.е. определена биологическая роль гена/белка) – менее 30%.
Применение современных методов анализа сверхбольших данных является приоритетным и, пожалуй, наиболее перспективным направлением исследований в области биоинформатики, математической и вычислительной биологии. Разрабатываемые в рамках алгебраического подхода методы анализа сверхбольших метрических конфигураций основаны на фундаментальных свойствах компактности и плотности метрических пространств, возникающих при формализации задач распознавания и классификации. Понятийный аппарат, вводимый в рамках разрабатываемого математического формализма, позволяет разрабатывать шкалируемые параллельные вычислительные алгоритмы для анализа «сгущений» точек в метрических конфигурациях большой размерности (миллионы, десятки миллионов точек).